#and you can use other functions for exponential growth and decay | Explore Tumblr posts and blogs

homeimprovementway · 1 year ago

Text

How to Use Calculator for Log: Master the Logarithm Functions

To use a calculator for log, simply press the "Log" button and enter the number. Logarithms help solve complex mathematical problems by finding the exponent for a given number. Logarithms are a fundamental mathematical concept with numerous applications in fields such as science, engineering, and finance. Using a calculator to compute logarithms can simplify complex calculations and help in problem-solving. By understanding how to use the log function on a calculator, individuals can efficiently determine the power to which a base must be raised to produce a specific number. This can aid in various scenarios, such as analyzing exponential growth or decay, calculating the time required for an investment to double, and solving equations involving exponential functions. Mastering the use of log on a calculator can enhance mathematical proficiency and streamline problem-solving processes in diverse academic and professional settings.

Using A Calculator

When it comes to solving logarithms, using a calculator can be a real time-saver. With the convenience of modern graphing calculators, you can easily calculate logarithms of any base, simplify complex equations, and perform calculations with small numbers. In this blog post, we will explore different ways to use a calculator for logarithms. Whether you are a student or a professional, this guide will help you make the most of your calculator's 'Log' button, enter logarithms on a graphing calculator, use other log bases, handle small numbers, and even divide natural logs with ease. Using The 'log' Button The 'Log' button on your calculator is specifically designed to calculate logarithms. To use it, simply enter the number you want to calculate the logarithm for and press the 'Log' button. The result displayed on your calculator is the exponent of the base number you entered. It's that simple! This feature is especially useful when you want to quickly find the logarithm of a number without manually performing complex calculations. Entering Logarithms On A Graphing Calculator If you're using a graphing calculator, entering logarithms is a little different. Most graphing calculators have a dedicated 'Log' button, usually located near the trigonometry functions. To calculate a logarithm on a graphing calculator, enter the base of the logarithm, followed by the value you want to find the logarithm of. For example, to calculate the logarithm base 10 of 100, you would enter "log(100,10)" into the calculator. The result will be displayed on the screen, giving you the logarithm of the specified number with the specified base. Using Other Log Bases Calculators usually default to base 10 logarithms. However, you may come across equations that require logarithms with different bases. Fortunately, most calculators allow you to enter logarithms with any base you desire. Simply use the log function followed by the base number in parentheses. For example, to calculate a logarithm base 2 of 8, enter "log(8,2)" into your calculator. The resulting value will be the logarithm of 8 with base 2. Using Logarithms With Small Numbers Working with small numbers can be tricky, but calculators make it much easier. To calculate the logarithm of a small number, simply enter the number as it appears in scientific notation. For example, if you want to find the logarithm of 0.001, you would enter "log(1 x 10^-3)" into your calculator. The calculator will then display the logarithm of the small number, giving you the solution you need. Dividing Natural Logs With A Calculator Dividing natural logs can be cumbersome, but with a calculator, it's a breeze. To divide natural logs, use the division operation ("/") and enter the two natural logs you want to divide. For example, to divide the natural log of 10 by the natural log of 2, you would enter "ln(10) / ln(2)" into your calculator. The result will be displayed on the screen, providing you with the answer to your division problem.

Tips And Tricks

When dealing with logarithms, there are various tips and tricks that can streamline the process and make calculations faster and more efficient. In this section, we will uncover some useful hacks that can help you quickly calculate logarithms without the need for a calculator. Quickly Calculate Logarithms Without A Calculator Calculating logarithms without a calculator can be simplified by utilizing a few strategic techniques. One method involves using the concept of inverses. Since logarithms are inverses of exponentials, you can utilize this relationship to simplify certain calculations. For example, if you need to find the logarithm of a number to a specific base, you can transform it into an exponential form and simplify the calculation. Another handy trick for quickly computing logarithms is to remember the common logarithm values. Having key logarithm values such as log 2, log 3, and log 5 memorized can aid in swiftly approximating logarithms of other numbers. Additionally, familiarizing yourself with the properties of logarithms, such as the product and quotient rules, can expedite the computation process and minimize the need for a calculator. https://www.youtube.com/watch?v=kqVpPSzkTYA

Calculating Logarithms On Different Calculator Brands

Calculating logarithms using different calculator brands can be a versatile skill. Below, we explore how logarithms can be calculated on various popular calculator brands. Using Logarithms On A Casio Calculator Calculating logarithms on a Casio calculator is straightforward. Follow these steps: - Press the "Log" button on your Casio calculator. - Enter the number you want to find the logarithm of. - Press the "=" button to display the result. Using Logarithms On An Iphone Calculator Utilizing logarithms on an iPhone calculator is convenient. Here's how you can do it: - Open the Calculator app on your iPhone. - Turn your iPhone to landscape mode to reveal the scientific calculator. - Tap the "Log" button followed by entering the number to calculate the logarithm. By following these simple steps, you can efficiently compute logarithms on your Casio calculator or iPhone calculator.

Frequently Asked Questions On How To Use Calculator For Log

How Do You Do Log On A Calculator? To calculate a logarithm on a calculator, press the "Log" button and enter the number you want to find the logarithm of. How Do You Do Log On A Normal Calculator? To find the logarithm on a normal calculator, press the "Log" button followed by the number. What Is The Easiest Way To Calculate Logs? The easiest way to calculate logs is using a calculator. Press the "Log" button, enter the number, and the result is the logarithm. How Do You Calculate Log10? To calculate log10, use a scientific calculator by pressing the "log" button and entering the number. The result displayed is the logarithm with base 10.

Conclusion

Using a calculator for logarithms can simplify complex calculations and save time. By following the steps outlined in this blog post, anyone can harness the power of logarithms in their mathematical endeavors with ease. So, go ahead, grab your calculator, and dive into the world of logarithms with confidence. Read the full article

0 notes

nebris · 6 years ago

Text

The Book No One Read

Why Stanislaw Lem’s futurism deserves attention.

I remember well the first time my certainty of a bright future evaporated, when my confidence in the panacea of technological progress was shaken. It was in 2007, on a warm September evening in San Francisco, where I was relaxing in a cheap motel room after two days covering The Singularity Summit, an annual gathering of scientists, technologists, and entrepreneurs discussing the future obsolescence of human beings.

In math, a “singularity” is a function that takes on an infinite value, usually to the detriment of an equation’s sense and sensibility. In physics, the term usually refers to a region of infinite density and infinitely curved space, something thought to exist inside black holes and at the very beginning of the Big Bang. In the rather different parlance of Silicon Valley, “The Singularity” is an inexorably-approaching event in which humans ride an accelerating wave of technological progress to somehow create superior artificial intellects—intellects which with predictable unpredictability then explosively make further disruptive innovations so powerful and profound that our civilization, our species, and perhaps even our entire planet are rapidly transformed into some scarcely imaginable state. Not long after The Singularity’s arrival, argue its proponents, humanity’s dominion over the Earth will come to an end.

I had encountered a wide spectrum of thought in and around the conference. Some attendees overflowed with exuberance, awaiting the arrival of machines of loving grace to watch over them in a paradisiacal post-scarcity utopia, while others, more mindful of history, dreaded the possible demons new technologies could unleash. Even the self-professed skeptics in attendance sensed the world was poised on the cusp of some massive technology-driven transition. A typical conversation at the conference would refer at least once to some exotic concept like whole-brain emulation, cognitive enhancement, artificial life, virtual reality, or molecular nanotechnology, and many carried a cynical sheen of eschatological hucksterism: Climb aboard, don’t delay, invest right now, and you, too, may be among the chosen who rise to power from the ashes of the former world!

Over vegetarian hors d’oeuvres and red wine at a Bay Area villa, I had chatted with the billionaire venture capitalist Peter Thiel, who planned to adopt an “aggressive” strategy for investing in a “positive” Singularity, which would be “the biggest boom ever,” if it doesn’t first “blow up the whole world.” I had talked with the autodidactic artificial-intelligence researcher Eliezer Yudkowsky about his fears that artificial minds might, once created, rapidly destroy the planet. At one point, the inventor-turned-proselytizer  Ray Kurzweil teleconferenced in to discuss, among other things, his plans for becoming transhuman, transcending his own biology to  achieve some sort of  eternal life. Kurzweil  believes this is possible,  even probable, provided he can just live to see  The Singularity’s dawn,  which he has pegged at  sometime in the middle of the 21st century. To this end, he reportedly consumes some 150 vitamin supplements a day.

Returning to my motel room exhausted each night, I unwound by reading excerpts from an old book, Summa Technologiae. The late Polish author Stanislaw Lem had written it in the early 1960s, setting himself the lofty goal of forging a secular counterpart to the 13th-century Summa Theologica, Thomas Aquinas’s landmark compendium exploring the foundations and limits of Christian theology. Where Aquinas argued for the certainty of a Creator, an immortal soul, and eternal salvation as based on scripture, Lem concerned himself with the uncertain future of intelligence and technology throughout the universe, guided by the tenets of modern science.

To paraphrase Lem himself, the book was an investigation of the thorns of technological roses that had yet to bloom. And yet, despite Lem’s later observation that “nothing ages as fast as the future,” to my surprise most of the book’s nearly half-century-old prognostications concerned the very same topics I had encountered during my days at the conference, and felt just as fresh. Most surprising of all, in subsequent conversations I confirmed my suspicions that among the masters of our technological universe gathered there in San Francisco to forge a transhuman future, very few were familiar with the book or, for that matter, with Lem. I felt like a passenger in a car who discovers a blindspot in the central focus of the driver’s view.

Such blindness was, perhaps, understandable. In 2007, only fragments of Summa Technologiae had appeared in English, via partial translations undertaken independently by the literary scholar Peter Swirski and a German software developer named Frank Prengel. These fragments were what I read in the motel. The first complete English translation, by the media researcher Joanna Zylinska, only appeared in 2013. By Lem’s own admission, from the start the book was a commercial and a critical failure that “sank without a trace” upon its first appearance in print. Lem’s terminology and dense, baroque style is partially to blame—many of his finest points were made in digressive parables, allegories, and footnotes, and he coined his own neologisms for what were, at the time, distinctly over-the-horizon fields. In Lem’s lexicon, virtual reality was “phantomatics,” molecular nanotechnology was “molectronics,” cognitive enhancement was “cerebromatics,” and biomimicry and the creation of artificial life was “imitology.” He had even coined a term for search-engine optimization, a la Google: “ariadnology.” The path to advanced artificial intelligence he called the “technoevolution” of “intellectronics.”

Even now, if Lem is known at all to the vast majority of the English-speaking world, it is chiefly for his authorship of Solaris, a popular 1961 science-fiction novel that spawned two critically acclaimed film adaptations, one by Andrei Tarkovsky and another by Steven Soderbergh. Yet to say the prolific author only wrote science fiction would be foolishly dismissive. That so much of his output can be classified as such is because so many of his intellectual wanderings took him to the outer frontiers of knowledge.

Lem was a polymath, a voracious reader who devoured not only the classic literary canon, but also a plethora of research journals, scientific periodicals, and popular books by leading researchers. His genius was in standing on the shoulders of scientific giants to distill the essence of their work, flavored with bittersweet insights and thought experiments that linked their mathematical abstractions to deep existential mysteries and the nature of the human condition. For this reason alone, reading Lem is an education, wherein one may learn the deep ramifications of breakthroughs such as Claude Shannon’s development of information theory, Alan Turing’s work on computation, and John von Neumann’s exploration of game theory. Much of his best work entailed constructing analyses based on logic with which anyone would agree, then showing how these eminently reasonable premises lead to astonishing conclusions. And the fundamental urtext for all of it, the wellspring from which the remainder of his output flowed, is Summa Technologiae.

The core of the book is a heady mix of evolutionary biology, thermodynamics—the study of energy flowing through a system—and cybernetics, a diffuse field pioneered in the 1940s by Norbert Wiener studying how feedback loops can automatically regulate the behavior of machines and organisms. Considering a planetary civilization this way, Lem posits a set of feedbacks between the stability of a society and its degree of technological development. In its early stages, Lem writes, the development of technology is a self-reinforcing process that promotes homeostasis, the ability to maintain stability in the face of continual change and increasing disorder. That is, incremental advances in technology tend to progressively increase a society’s resilience against disruptive environmental forces such as pandemics, famines, earthquakes, and asteroid strikes. More advances lead to more protection, which promotes more advances still.

And yet, Lem argues, that same technology-driven positive feedback loop is also an Achilles heel for planetary civilizations, at least for ours here on Earth. As advances in science and technology accrue and the pace of discovery continues its acceleration, our society will approach an “information barrier” beyond which our brains—organs blindly, stochastically shaped by evolution for vastly different purposes—can no longer efficiently interpret and act on the deluge of information.

Past this point, our civilization should reach the end of what has been a period of exponential growth in science and technology. Homeostasis will break down, and without some major intervention, we will collapse into a “developmental crisis” from which we may never fully recover. Attempts to simply muddle through, Lem writes, would only lead to a vicious circle of boom-and-bust economic bubbles as society meanders blindly down a random, path-dependent route of scientific discovery and technological development. “Victories, that is, suddenly appearing domains of some new wonderful activity,” he writes, “will engulf us in their sheer size, thus preventing us from noticing some other opportunities—which may turn out to be even more valuable in the long run.”

Lem thus concludes that if our technological civilization is to avoid falling into decay, human obsolescence in one form or another is unavoidable. The sole remaining option for continued progress would then be the “automatization of cognitive processes” through development of algorithmic “information farms” and superhuman artificial intelligences. This would occur via a sophisticated plagiarism, the virtual simulation of the mindless, brute-force natural selection we see acting in biological evolution, which, Lem dryly notes, is the only technique known in the universe to construct philosophers, rather than mere philosophies.

The result is a disconcerting paradox, which Lem expresses early in the book: To maintain control of our own fate, we must yield our agency to minds exponentially more powerful than our own, created through processes we cannot entirely understand, and hence potentially unknowable to us. This is the basis for Lem’s explorations of The Singularity, and in describing its consequences he reaches many conclusions that most of its present-day acolytes would share. But there is a difference between the typical modern approach and Lem’s, not in degree, but in kind.

Unlike the commodified futurism now so common in the bubble-worlds of Silicon Valley billionaires, Lem’s forecasts weren’t really about seeking personal enrichment from market fluctuations, shiny new gadgets, or simplistic ideologies of “disruptive innovation.” In Summa Technologiae and much of his subsequent work, Lem instead sought to map out the plausible answers to questions that today are too often passed over in silence, perhaps because they fail to neatly fit into any TED Talk or startup business plan: Does technology control humanity, or does humanity control technology? Where are the absolute limits for our knowledge and our achievement, and will these boundaries be formed by the fundamental laws of nature or by the inherent limitations of our psyche? If given the ability to satisfy nearly any material desire, what is it that we actually would want?

Lem’s explorations of these questions are dominated by his obsession with chance, the probabilistic tension between chaos and order as an arbiter of human destiny. He had a deep appreciation for entropy, the capacity for disorder to naturally, spontaneously arise and spread, cursing some while sparing others. It was an appreciation born from his experience as a young man in Poland before, during, and after World War II, where he saw chance’s role in the destruction of countless dreams, and where, perhaps by pure chance alone, his Jewish heritage did not result in his death. “We were like ants bustling in an anthill over which the heel of a boot is raised,” he wrote in Highcastle, an autobiographical memoir. “Some saw its shadow, or thought they did, but everyone, the uneasy included, ran about their usual business until the very last minute, ran with enthusiasm, devotion—to secure, to appease, to tame the future.” From the accumulated weight of those experiences, Lem wrote in the New Yorker in 1986, he had “come to understand the fragility that all systems have in common,” and “how human beings behave under extreme conditions—how their behavior when they are under enormous pressure is almost impossible to predict.”

To Lem (and, to their credit, a sizeable number of modern thinkers), the Singularity is less an opportunity than a question mark, a multidimensional crucible in which humanity’s future will be forged.

I couldn’t help thinking of Lem’s question mark that summer in 2007. Within and around the gardens surrounding the neoclassical Palace of Fine Arts Theater where the Singularity Summit was taking place, dark and disruptive shadows seemed to loom over the plans and aspirations of the gathered well-to-do. But they had precious little to do with malevolent superintelligences or runaway nanotechnology. Between my motel and the venue, panhandlers rested along the sidewalk, or stood with empty cups at busy intersections, almost invisible to everyone. Walking outside during one break between sessions, I stumbled across a homeless man defecating between two well-manicured bushes. Even within the context of the conference, hints of desperation sometimes tinged the not-infrequent conversations about raising capital; the subprime mortgage crisis was already unfolding that would, a year later, spark the near-collapse of the world’s financial system. While our society’s titans of technology were angling for advantages to create what they hoped would be the best of all possible futures, the world outside reminded those who would listen that we are barely in control even today.

I attended two more Singularity Summits, in 2008 and 2009, and during that three-year period, all the much-vaunted performance gains in various technologies seemed paltry against a more obvious yet less-discussed pattern of accelerating change: the rapid, incessant growth in global ecological degradation, economic inequality, and societal instability. Here, forecasts tend to be far less rosy than those for our future capabilities in information technology. They suggest, with some confidence, that when and if we ever breathe souls into our machines, most of humanity will not be dreaming of transcending their biology, but of fresh water, a full belly, and a warm, safe bed. How useful would a superintelligent computer be if it was submerged by storm surges from rising seas or dis- connected from a steady supply of electricity? Would biotech-boosted personal longevity be worthwhile in a world ravaged by armed, angry mobs of starving, displaced people? More than once I have wondered why so many high technologists are more concerned by as- yet-nonexistent threats than the much more mundane and all-too-real ones literally right before their eyes.

Lem was able to speak to my experience of the world outside the windows of the Singularity conference. A thread of humanistic humility runs through his work, a hard-gained certainty that technological development too often takes place only in service of our most primal urges, rewarding individual greed over the common good. He saw our world as exceedingly fragile, contingent upon a truly astronomical number of coincidences, where the vagaries of the human spirit had become the most volatile variables of all.

It is here that we find Lem’s key strength as a futurist. He refused to discount human nature’s influence on transhuman possibilities, and believed that the still-incomplete task of understanding our strengths and weaknesses as human beings was a crucial prerequisite for all speculative pathways to any post-Singularity future. Yet this strength also leads to what may be Lem’s great weakness, one which he shares with today’s hopeful transhumanists: an all-too-human optimism that shines through an otherwise-dispassionate darkness, a fervent faith that, when faced with the challenge of a transhuman future, we will heroically plunge headlong into its depths. In Lem’s view, humans, as imperfect as we are, shall always strive to progress and improve, seeking out all that is beautiful and possible rather than what may be merely convenient and profitable, and through this we may find salvation. That we might instead succumb to complacency, stagnation, regression, and extinction is something he acknowledges but can scarcely countenance. In the end, Lem, too, was seduced—though not by quasi-religious notions of personal immortality, endless growth, or cosmic teleology, but instead by the notion of an indomitable human spirit.

Like many other ideas from Summa Technologiae, this one finds its best expression in one of Lem’s works of fiction, his 1981 novella Golem XIV, in which a self-programming military supercomputer that has bootstrapped itself into sentience delivers a series of lectures critiquing evolution and humanity. Some would say it is foolish to seek truth in fiction, or to draw equivalence between an imaginary character’s thoughts and an author’s genuine beliefs, but for me the conclusion is inescapable. When the novella’s artificial philosopher makes its pronouncements through a connected vocoder, it is the human voice of Lem that emerges, uttering a prophecy of transcendence that is at once his most hopeful—and perhaps, in light of trends today, his most erroneous:

“I feel that you are entering an age of metamorphosis; that you will decide to cast aside your entire history, your entire heritage and all that remains of natural humanity—whose image, magnified into beautiful tragedy, is the focus of the mirrors of your beliefs; that you will advance (for there is no other way), and in this, which for you is now only a leap into the abyss, you will find a challenge, if not a beauty; and that you will proceed in your own way after all, since in casting off man, man will save himself.”

Freelance writer Lee Billings is the author of Five Billion Years of Solitude: The Search for Life Among the Stars.

https://getpocket.com/explore/item/the-book-no-one-read

Summa Technologiae https://publicityreform.github.io/findbyimage/readings/lem.pdf

#The Sisterhood

12 notes · View notes

thievesgambit-a · 7 years ago

Text

headcanon 009: the science behind remy’s powers

thank @p-sychofreak for making me think about this harder and writing it down because i was mostly avoiding it because there’s a reason i decided to leave the physics department at my school.

so what comics say is “gambit’s powers is turning an object’s potential energy into kinetic energy and making shit explode” which is..........dumb because that’s really.....bullshit. I prefer to think of it as remy can accelerate the movement of atoms in inorganic material (and, without Sinister’s surgery, organic material, and can do it telekinetically, but the science still stands). and, in any case, this is what his “actual” counterpart, New Son or New Sun, has been described as being able to do (i.e. manipulating particles at a quantum level), so basically it’s canon and i’m right.

there’s some science shit under the cut, although i’m not going to explain everything because.......that would take a lot of effort (there’s a few aspects of chemistry and physics that I don’t feel like going into for a random ass headcanon post on tumblr rn). I’ll link some wiki pages at the end if you REALLY wanna know, and you can talk to me if you REALLY wanna talk it out. but basically: the greater the surface area, the bigger the explosion by an exponential factor rather than a linear one (but more time to charge, obviously).

so when electrons are excited, they jump from energy level to energy level (i.e. the rings around the nucleus in atom pictures), they release photons (i.e. light particles) and radiation. the increase in energy also releases some heat, which is true in any transfer of energy (see: headcanon 007). so what Remy is really doing when he “charges” an object is accelerating its atoms until electrons have bounced out of the energy levels in atoms and away from their nuclei, thus making the particles highly unstable and thus triggering an explosion on impact or after a specific amount of time (at which point the atoms break down and explode). Remy has developed an instinctual gauge on how much he needs to charge objects he’s used to (like his playing card) in order to explode in a certain amount of time.

this makes his explosions and objects he charges actually more nuclear in nature, because they depend on cascading electrons and the unstable reactions in the material. however, because the objects are so small, I wouldn’t really say the amount of radiation is very dangerous--and I really wouldn’t say Remy is dangerously radioactive, himself. yeah, he seeps radiation, but honestly, so do the rest of us. his is just minutely greater than everyone else’s.

anyways. so that’s what his power is doing. obviously, there’s some magic mutant bullshit in there, because I for one have never heard of scientists trying to heat objects so much that they explode.

I also believe that, the greater the surface area of the object he is charging, the greater the explosion--and the strength of the explosion grows exponentially rather than linearly. that is to say, an object that has twice the surface area of a playing card might have quadruple the explosion strength at full charge (this is just an approximation/example).

in idealized black bodies, which are objects that absorb all radiation and energy, their heat and radiation levels increase exponentially depending on their surface area (and later drop off after a certain frequency in the applied wave is reached). the general equation for this is referred to the Planck’s law. most metals can be considered black bodies--although not pure ones, since there’s usually random shit in them. but, you know that metal spoon that heats up when you leave it in your soup for too long, or how your bowls get hot if you leave them in the microwave for a while? black body radiation.

anyways, you can think of Planck’s law as describing how many photons an object is giving off, or how much energy the object is giving off in the form of radiation. the more energy you put in, the more radiation you get. as you can see from the helpful example curves Wikipedia provides, the growth and decay are exponential (which can also be seen clearly from the units and the equation provided, themselves).

notice that the final units of the radiation (i.e. Bν) of the blackbody have inverse unit meters squared (i.e. the area of the object). "unit” refers to 1 of something--in this case, 1 square meter of the object. depending on the frequency, wavelength, and other factors of the energy going into the object, its power can change. that means that, for two square unit meters of the item, the power is doubled, and for three, tripled, etc.

but remember that the equation itself is exponential, which means we have a (f3/2(x))(SA-1), where SA is the surface area (to the inverse, because that's where the units go) and f(x) is some function that is raised to an exponential (i.e. Planck’s law). clearly, then, the ultimate function is exponential in nature. because the greater the area, the less the ultimate explosion, Remy needs to put in more energy and power to get the same amount of explosion--but then again, since it's a greater surface area, usually it can hold more energy, and he continues to increase the radiation and instability in the object. because electrons tend to react off of each other at an exponential rate releative to how much of them there are, the power increases exponentially as well.

if you look at the Wiki, the growth isn’t infinite--which is great, because that would break physics on a couple of levels that I won’t get into. so Remy instinctively has the ability to use the appropriate level of power or just below it so he does not reach that drop off point, although he does not consistently hit the peak radiation levels either. and, with objects he is less familiar with, he is more likely to fuck up the amount of energy he has to put in.

obviously, this is all pseudo science and some bullshitting on my part, because on some level I don’t want to think too hard because it’s fucking mutant superpowers and this will never happen in real life and trying to explain it scientifically is a dumb idea to me because like this isn’t even science but if it was kinda sciencey then this is the shit I would say.

if you’re a physics or chem person and see all the shit that’s bullshitted in this don’t @ me like i know. i don’t feel like rationalizing it it’s fucking comics dude let me live.

#❛ ♠ ⁞ it’s all in the cards — headcanons #i also haven't done physics in like 3 years b/c i left that department for writing #b/c writing is easier LMAO #anyways i didn't take higher level quantum so don't attack me

2 notes · View notes

gilliansmb · 4 years ago

Text

Blog Entry # 7: Functions as Mathematical Models

This week’s lesson is a continuation of last week’s lesson on functions.

This week, we are tasked to learn about functions as mathematical models. This has been a topic introduced to us in Grade 10, so I can say that I have a bit of familiarity to this topic.

We have three learning guides to learn this week, and out of those three, I understood the third module (about exponential growth) the least, probably because this was the topic we did not touch on the most in Grade 10 because it was discussed to us during the bridging program.

Nonetheless, I practiced solving problems from the given learning guides.

These are my answers to questions from all three learning guides that I have checked. As I said, learning guide 3 took me the longest since I still had to watch multiple videos explaining the process.

In conclusion, I think that this lesson was fun and quite challenging even though I can consider it a review of lessons from the past since I think I have learned additional knowledge about it. I think I can use my knowledge about this in the future for seeing when certain foods expire, management of expenses, and even relating to other subjects like Biology (for calibrating evolutionary clocks) and Chemistry (bacterial decay)

That’s it from me this week. See you on the next blog entry ヾ(•ω•`)o

0 notes

personalcoachingcenter · 4 years ago

Text

Research Paper: Complex Dynamic Systems Coaching Theory

New Post has been published on https://personalcoachingcenter.com/research-paper-complex-dynamic-systems-coaching-theory/

Research Paper: Complex Dynamic Systems Coaching Theory

Research Paper By Bianca Prodescu (Systems Coach, NETHERLANDS)

Systems coaching is becoming a popular trend, due to the need of pursuing long-lasting changes in the behavior that do not negatively impact other parts of the client’s life. The aim is to look beyond quick solutions that only target symptoms and scarce attempts to change aimed to the edge of the comfort zone which is immediately absorbed.

In systems coaching, the approach is moving from seeing the coaching relationship as a one-to-one cause-effect solution exploration, towards understanding the client’s relationships system: the team, the department, the family, etc. with the intent of creating awareness and visibility of the impact the environment has on the client.

There is still the risk of a simplistic view approach: that the individual is seen as an independent agent within a system that can be fully defined and contained. Thus giving the client the impression that they can engineer any desired change.

This paper aims to present the reader with an understanding of the systems theory and how complex is the nature of human behavior, followed by a specific example to illustrate how it can be applied to coaching individuals.

Complex adaptive systems

A complex system consists of multiple active different parts known as elements, distributed out without centralized control, connected. At some critical level of connectivity, the system stops being just a set of elements and becomes a network of connections. As the information flows through the network, the parts influence each other and they start to function together as an entity. A global pattern of organization emerges.

The interactions between the elements are non-trivial or non-linear. For example, if all the parts in a car are arranged in a specific way, then we will have the global functionality of a vehicle. A system’s behavior is caused by its structure, not its individual parts.

For example, a colony of ants – each ant on its own has a very simple, observable behavior, while the colony can work together to accomplish very complex tasks without any central control. They can organize themselves to produce outputs that are significantly greater than any individual can produce alone.

As a system at a new level is being developed, it starts to interact with other systems in its environment. People form part of social groups that form part of broader society which in turn forms part of humanity. A business is part of a local economy, which is part of a national economy, which in turn is part of the global economy.

These elements are nested inside of subsystems which in turn can form larger systems, where each subsystem is interconnected and interdependent with the others. This is a primary source of complexity.

Complex systems emerge to serve specific purposes, and the journey towards achieving that drives their behavior. The systems adapt based on whether they are reaching their goals, which makes them dynamic.

In complex dynamic systems, causality goes both ways: the environment can affect their behavior and the system’s behavior change can affect the environment. Due to these feedback loops, the system may decay or grow at an exponential rate.

There is no formal definition of what a complex system is, but it can be described by properties:

Made out of elements that are considered simple relative to the whole;

Interdependence and non-linearity;

Connectivity: the nature and structure of these connections define the system as opposed to the individual properties of its elements. “What is connected to what?” and “How are things connected?” become the main questions. As the number of connections between elements can grow exponentially, complexity grows.

Autonomy and self-organization: no top-down, central control, the system can organize itself in a decentralized way. As the system accepts information from the environment, it uses the information to make decisions about what actions to take. The components don’t gain the information or make the decisions individually; the whole system is responsible for this type of information processing. Self-organizing systems rely on the short feedback loops to generate enough states that can be tested to find out the appropriate response to a perturbation. A downside of this is that these feedback loops reduce diversity, and all elements of the system can become susceptible to the same perturbation results in a large shock that can lead to the destruction of the system. Therefore variation and diversity are requisite to the health of the system. [Kaisler and Madey, 2009].

Adaptiveness: how the system changes in its patterns in space and time to either maintain or improve its function depending on the goal.

Emergent behavior: coordination in such systems is formed out of the local interactions that give rise to the overall organization. This general process is called emergence.

Behavior cannot be derived from the individual components but the collective outcome of the system. Emergent behaviors have to be observed and understood at the system level rather than at the individual level. Within a complex system, we do not search for global rules that govern the whole system, but instead how local rules give rise to the emergent organization.[Johnson et al., 2011]

You cannot understand a complex system by examining each part and adding it all up. To understand a system you need to understand the goal and the structure underlying it and the interactions with other systems and agents.

Application to coaching

When to apply systems thinking in coaching

A significant change is either happening or needs to take place.

It’s not a one-off event.

Multiple perspectives become apparent when observing the situation.

The client has tried addressing it before, without finding a way to keep it from recurring.

There is no obvious solution.

A previous attempt to address it has created problems elsewhere.

The growth experienced by focusing on one area leads to a decline in another area.

There is more than one impediment to growth in the desired area.

Growth slows down over time.

Over time there is a tendency to settle for less than the initial starting position.

The same solution is used repeatedly with decreased effectiveness over time.

But human beings are not ants, all acting according to standard rules. They are emotional, erratic, spontaneous, and conscious, capable of observing the pattern of interactions that they are contributing towards.

Therefore, when coaching an individual you cannot classify them as a collection of independent behaviors and actions and approach them as an isolated system in which you can control and predict the behavior.

Stacey and Mowles (2016) suggest that it is better to focus on the process of human interaction and how to develop the approach towards change.

As a coach, it is important to look beyond their behavior to understand the events and how the nature of interpersonal dynamics impacts the client. Help the client recognize and accept that change occurs in situations of ambiguity and high uncertainty.

As seen above, emergence plays an important role in a complex system. Due to this property, knowing the starting state does not allow you to predict the mature form of the system, and knowing the mature form does not allow you to identify the initial state. The only way to figure it out is to go through the whole development process step by step, understand the goal and the structure underlying it, and the interactions with other systems and agents.

In coaching, this translates to supporting the client during the self-awareness process that a goal is not a plan but a hypothesis in progress that can change anytime under the influence of their own actions or the environment they are part of.

An emergent property of organic complex adaptive systems is resilience, the ability to react to perturbations and environmental events by absorbing, adapting to, and recovering from disruptions.

According to Holling’s seminal study, “resilience determines the persistence of relationships within a system and is a measure of the ability of these systems to absorb changes of state variables, driving variables, and parameters, and persist”.

In a coaching context, we define resilience as the ability to emotionally cope with adversity, recover, adapt, or persevere.

If the disturbance is minor, the system can absorb it and recover. To drive substantial change, the system has to receive an impact big enough to disturb the capacity of the system to return to an equilibrium state. That’s why major life events that disturb our daily routines and our values system can give the best opportunity for making long term changes.

The coach should also be aware of the observer effect and understand they are now part of the client’s system and their own behavior, choice of wording, inflection and intonation will have an impact. As well as that the coach themselves is not a free independent agent and may suffer changes in their own behavior as a response to the interaction with the client.

Small changes can produce big results—but the areas of highest leverage are often the least obvious (Peter Senge, The Fifth Discipline, 2006). Also in the quest of supporting the client to embrace change, the small steps approach has proven to give sustainable results. In the following section, we will explore the impact a small-step approach to change has on the human brain.

Why small steps?

Our behavior is shaped by experiences and the environment around us.

Any small experience can reinforce or challenge our beliefs. Our beliefs determine how we act to get the most motivating result. The outcome of our actions is used as feedback for our brain to categorize the initial experience as a positive or negative one.

Our brains learn early on what works and what doesn’t. While in infancy the brain is malleable, as we become adults our brain creates routines and frameworks aimed at survival. As our habits become embedded in neural pathways, introducing new behaviors becomes challenging.

When change occurs it introduces a deviation from the plan created by learning from the past, and the uncertainty created by it sends our brain into stress.

The default response is to be on guard for potential risks and the main question our brain is now trying to answer is “How do I minimize the threat?”

The bigger the goal – the bigger the change – the bigger the risk – the more our brain opposes the change.

Thus the key to making the brain get used to change and maintain self-awareness is to recognize upfront when a task is too big. Then focus on a smaller initial step and map out the knowledge you want to gather by executing that step.

This works two-fold: it minimizes the impact of the failure and helps identify the value failure can bring.

It doesn’t mean that the changes should happen slowly, but to recognize that continuous and incremental improvement adds up to bigger changes in the future that have a positive impact.

Small steps that reward the effort with learning become perceived as a success. A couple of small successes slowly challenge our beliefs, our values, and slowly our behavior.

Therefore when a big life-changing event happens, having a small steps approach helps with minimizing the perceived risk.

Case study

From senior to the leader

The client had been in his current position for several years, struggling to get recognition for his seniority and advance in a leadership position. The lack of visible recognition not only inhibited him from showing the expected behavior but also triggered other behavior that detracted from his growth.

This case is an example of negative reinforcing loops between the behavior and the environment.

The approach was to first encourage the coachee to seek out different perspectives to further understand the situation, by engaging first in a self-reflective session and then with others in other reflective practices (personal review, 360-degree feedback sessions, and shadowing the coachee to provide an objective view).

Taking a collaborative approach helps the coachee steer away from a single source of truth and have a better understanding of the social tensions in the relationships with others.

The trigger for change was in the end the result of this collaborative exploration, where the input from all respondents converged around the same points. The outcome of the first coaching session was acknowledging the feedback received, understanding their own limits, and how much more they were willing to persist in the current situation. This led to making a time-bound resolution: operate from within a leadership position within 6 months.

From a complex systems point of view it meant that if either one of the reinforcing loops could be tampered with, the change in behavior or the change in environment, the client would benefit. The client considered two extreme solutions that could be fully within their control, but with big side implications: giving up the leadership role or take on the role in a different company. As we have seen in the theoretical analysis, big changes can impair a person from persevering in their set resolution, so they were marked as last resort actions at the end of the 6 months journey.

The intermediate approach was to address both loops at the same time to identify the weakest link. Therefore a high-level mapping aimed at the behavior the client wanted to address, the current social interactions, and their respective outcomes in terms of thoughts, feelings, and reactions would help identify the smallest step to take. The main role of the coach here was to create awareness that human nature is too complex and unpredictable to be able to fully model it and to spend just enough time at this step to provide a first self-awareness moment.

The insights gained at this point were that the main detractors were: hierarchy and lack of clarity in expectations, as seen in the map below.

The coachee drew the insight that the hierarchical nature of a relationship created a barrier that impeded him from proactively approaching those specific people, even when the frustration levels were high. Thinking about what those people should provide for him because of position, how they should behave towards him, how they viewed him, how much their time he was worth etc. made the client feel that if his situation was important, the responsibility to address it was on the other person.

When this insight was put in balance with the goal stated at the beginning, the client decided to switch the responsibility of triggering the process towards him and to share the solution with the key stakeholders in his systems’ network.

To understand how this would be a feasible consistent approach, the main motivators were identified: tangible, observable results in respect to the efforts made, which would then enable external recognition.

The main supporting structures were identified as: people in leadership positions with which a good rapport was already built, taking small actions directed towards clarifying the expectations, and external and recurring accountability for the actions.

The exploration of the supporting structures also gave way to identifying the first opportunity in weakening the detracting loops: clarifying the expectations with leaders that the coachee already had a trusting rapport built, where the perceived hierarchy load was low.

This action had multiple effects:

Since the barrier to approach someone was lower, the coachee had the opportunity to address it quickly, which gave fast results;

As some of the expectations were clarified, the results had a positive value/effort ratio and increased the coachee’s confidence both in showing the expected behavior and in the approach;

The coachee identified the prerequisites of the smallest step they were most likely to complete, and that the most important of them was the kind of rapport they had with the other person.

As they kept exploring the social relationships with other key stakeholders, the need of addressing the change in the environment to support consistent growth became apparent.

In line with the learnings from the previous actions, the coachee took a small step together with a manager that both had a trusting rapport with the client and the authority to trigger a change in the environment.

By formalizing the clarified expectations and having them shared with the other stakeholders in the client’s network a change in the dynamics of the environment took place.

The most impactful one being that now other agents within the system would trigger the process. This lowered the threshold of starting the conversation about clarifying expectations with some people and created more opportunities where he could showcase the desired behavior, offering an increase in self-confidence and the external recognition became noticeable.

By the end of the 6 months journey, the client had managed to successfully challenge both loops and significantly loosen the cause-effect relationship between them. The client identified that similar situations were now visible within the personal environment, which is proof that you cannot treat a case in isolation. Recognizing the impact triggered an exploration of their social identity and helped the client make explicit the attributes of the environment in which they can be at their best.

He summarized the following learnings about his approach to change:

How to recognize that change is either happening or needs to happen: when the build-up of frustration is visible to the outside and taking a moment every two weeks to reflect if a frustration showed up several times;

How to approach the change: “If I am not doing it, then it means it’s too big” translated to small, bite-sized actions that loosen the pressure from having the right solutions from the beginning;

What is the so-called safe environment for exploration and learning: a network of people with a low hierarchical load that can provide valuable, judgment-free feedback and opportunities for exploring solutions;

The type of actions that would qualify as low risk but valuable: What’s the worst that could happen? What’s the learning I am aiming to get from this step?

As a coach, at the request of the client, I played, in the beginning, the role of keeping external accountability for the actions. I noticed that my presence during the shadow-coaching sessions reinforced the specific actions discussed during the individual coaching sessions. Here I could observe firsthand the impact I had on the client’s system and brought me the realization that I was creating a dependency relationship.

Overall this experience was in line with the small steps theory for change, where we saw that a small change in an input value to the system can, through feedback loops, trigger a large systemic effect.

When applying complex dynamic systems theory as a coach, you can support your client to acknowledge that they are part of a network system of a multitude of dynamic and continuously evolving relationships. To identify their own patterns for thinking, to identify assumptions and perceptions. To clarify their role as an individual and as part of a bigger context. To support them in getting comfortable with uncertainty by understanding that their role is not to try and direct events, but to participate with intent and purpose in relationships in service of learning how to navigate the power dynamics so they can be at their best.

References

Beer, S. (1975). A Platform for Change. New York: John Wiley & Sons Ltd.

Clemson, B. (1991). Cybernetics: A New Management Tool. Philadelphia: Gordon and Breach.

Davidson, M. (1996). The Transformation of Management. Boston. Butterworth-Heinemann.

Imagine That Inc

Goodman, M. & Karash, R. & Lannon, C. & O’Reilly, K. W., & Seville, D. (1997). Designing a Systems Thinking Intervention. Waltham, MA. Pegasus Communications, Inc.

isee Systems (Previously High-Performance Systems).

Strategy Dynamics Inc.

O’Connor, J. (1997). The Art of Systems Thinking: Essential Skills for Creativity and Problem Solving. London: Thorsons, An Imprint of HarperCollins Publishers.

Richmond, B. (2001). An Introduction to Systems Thinking. Hanover, NH. High-Performance Systems.

Senge, P. (1990). The Fifth Discipline: The Art & Practice of The Learning Organization. New York: Doubleday Currency.

Vensim PLE & Vensim. Ventana Systems.

Warren, K. (2002). Competitive Strategy Dynamics. West Sussex, England. John Wiley & Sons.

https://www.researchgate.net/publication/337574336_What_is_Systemic_Coaching

Resilience in Complex Systems: An Agent‐Based Approach

Original source: https://coachcampus.com/coach-portfolios/research-papers/bianca-prodescu-complex-dynamic-systems-theory-applied-to-coaching/

0 notes

cladeymoore · 5 years ago

Text

Things You Need to Know about the Bitcoin Halving, Ethereum’s Competitors Nearing Launch, and…

Things You Need to Know about the Bitcoin Halving, Ethereum’s Competitors Nearing Launch, and other Crypto News

Coinbase Around the Block sheds light on key issues in the crypto space. In this edition, we reveal key takeaways from the upcoming Bitcoin halving as well as Ethereum’s newest competition.

A Lead Up to the 3rd Bitcoin Halving

To date, Bitcoin has undergone two halvings (2012 and 2016), and we are quickly approaching the third.

For background, Bitcoin pioneered a deflationary economic model by setting an upper limit of 21 million bitcoins. In order to spur adoption, issuance was initially set at 50 BTC per block (every 10 minutes), and set to decay in half every four years as the network presumably grows more valuable. This event is now colloquially dubbed the halving.

Today, 18M Bitcoin have already been mined (86% of the final supply), with 12.5 new BTC (~$125K) issued every block. This will drop in May 2020 to 6.25 BTC (~$63K).

In inflationary terms, this moves Bitcoin from ~3.6% annual inflation to 1.7%, less than USD’s target inflation (2%) and roughly on par with Gold, potentially strengthening the narrative of Bitcoin as digital gold — a new kind of store of value.

Bitcoin Monetary Inflation and Halvings

Graph from BashCo.github.io

Following simple supply and demand analysis, each halving decreases supply, and is commonly believed to be a driver for increased price. But what has happened in past halvings, and what can we learn?

BTC’s Momentum After Past Halvings

Bitcoin’s 1st halving occurred in early 2012, when the Bitcoin ecosystem was small, fragile, and volatile.

Following a long sideways market in 2012, the 1st halving itself was anticlimactic but was followed a few months later by a significant bull market. Smashing new all time highs and setting Bitcoin up for an explosive end to 2013, crossing $1300.

Fast forward 4 years, once again Bitcoin was in a long sideways market after falling from the $1300 peak in 2013. The halving itself was again nondescript, but bitcoin began to build strong momentum ~6 months later leading to the unprecedented 2017 run.

3rd Halving on the Horizon

Following the first two halvings, we note that most of the exponential growth occured after the halving. In fact, in each circumstance the halving itself was more of a non-event and any possible impact took ~3–6 months to appear.

Today, for a 3rd time we are in the midst of a long sideways market leading into the halving (although 2019 did see a mini run in the middle, but has since tapered off).

But notably different from past halvings, the crypto ecosystem has significantly matured. Crypto services have made it simple to buy, hold, and use Bitcoin, giving easy access to anyone who wants exposure. On the other hand, it’s also much easier to bet against Bitcoin and go short (via margin, futures, and derivatives). This was difficult in 2016, and completely absent in 2012.

Compared to 2016, crypto has also gained widespread notoriety. Most people have at least heard of bitcoin, and a number of institutions have (at minimum) developed an internal perspective on this asset class.

So is the halving priced in? There are generally two schools of thought:

Yes. The halving is a byproduct of Bitcoin’s public and well-known economic model. All public information is priced-in to efficient markets, and this is no different.

No. The halving is a narrative more than anything else, and may influence demand more than supply by driving increased awareness and adoption.

Key Takeaways for the upcoming BTC Halving

Studying prior Bitcoin halvings is a fascinating insight into market behavior and the evolution of Bitcoin as a new asset class. What will happen during and after the next halving? Anyone predicting the future is ultimately guessing, so we’ll have to wait and see. At minimum, the coming halving should produce a strong current of Bitcoin press, opinions, and theories.

Overview on Ethereum Competitors Nearing Launch

Throughout 2015–2017, several projects raised funds to develop general purpose smart-contract blockchain platforms, owing to 1) perceived market demand; 2) technical differentiators they might develop; and 3) expected challenges Ethereum might encounter.

It quickly became apparent that building novel smart-contract platforms is exceedingly complex, and nearly all platforms experienced significant delays (including ETH 2.0). Today, some of the most anticipated platforms are finally on the cusp of deployment.

Here’s an overview of some upcoming projects:

DFINITY

DFINITY aims to build a decentralized “Internet Computer,” where they would enable the public Internet to natively host backend software, transforming it into a global compute platform. Internet services would then be able to install their code directly on the public internet and dispense with all servers, cloud services, and centralized databases.

There are many implications to this idea, notably revolving around decentralizing the web and enabling open innovation, but also creating a path to autonomous software such as open versions of Facebook or LinkedIn. As a side-effect, it may also carry potentially improved security models and remove IT complexities and costs, among other things. If successful, this would be a powerful paradigm shift in how the internet operates.

To accomplish this, DFINITY has assembled a strong team of technologists and published some breakthroughs in consensus mechanisms to enable larger throughput (Threshold Relay).

Polkadot

Polkadot targets building an interoperability network, aiming to enable blockchain projects to:

Trustlessly transfer assets between different chains;

Enable cross-chain smart contracts that can interact with each other; and

Provide a framework to quickly spin up application-specific chains that can be used by other blockchains.

Interoperability is a key building block for the crypto ecosystem. By way of example, it could enable crypto-kitties to create a specific blockchain with massive throughput (so you can breed those kittens as fast as you want), but your crypto-kitties could be accessed by Ethereum, and your platform could use ETH, Dai, or any other ERC-20 token (or possibly ETH infrastructure) natively.

The early days of web servers may be a helpful analogy. Back then, a single server hosted several web pages. If any page exploded in popularity, it slammed the whole server and took down all other web pages with it. The internet evolved to segregated, application-specific servers enabling each web page to scale as needed, without impacting anyone else. Replace web pages with blockchains, and this is just one aspect of what interoperability and application specific chains might do for crypto.

Polkadot is led by Gavin Wood (co-founder of Ethereum) via Parity. Their approach is conceptually similar to Cosmos, but differentiated in how their interoperability network handles security.

NEAR Protocol

NEAR is similar in vision to Ethereum 2.0: A proof-of-stake, sharded blockchain with smart contract functionality, but with a twist in consensus design that better protects composability — or the ability for smart contracts to seamlessly interact with each other across shards. Coinbase Ventures is an investor in NEAR.

The NEAR team, a collection of ICPC medalists, believe targeting dapp developers is critical to long-term traction and are emphasizing the developer experience. Their goal is to launch a truly scalable chain with seamless developer tooling and with a built-in ETH → NEAR bridge so end-users can still use ETH tokens (and possibly ETH infrastructure), which would lower barriers to adoption.

In essence, NEAR is similar to ETH 2.0 but built on a new chain and new environment, thus forfeiting some of the significant network effects ETH has acquired. NEAR is planning a launch in Q2 this year.

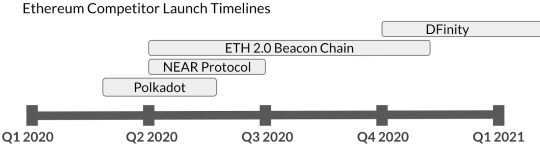
Takeaways

Each ETH competitor also faces an uphill climb competing against the strong network effects Ethereum has accrued around infrastructure, tooling, distribution, and mindshare.

In the end, each new protocol’s launch is simply the beginning of a much longer journey. And in the long run, these networks could add new functionality to the wider crypto protocol layer, broadening the crypto design space and increasing the potential for impactful dapps.

This website contains links to third-party websites or other content for information purposes only (“Third-Party Sites”). The Third-Party Sites are not under the control of Coinbase, Inc., and its affiliates (“Coinbase”), and Coinbase is not responsible for the content of any Third-Party Site, including without limitation any link contained in a Third-Party Site, or any changes or updates to a Third-Party Site. Coinbase is not responsible for webcasting or any other form of transmission received from any Third-Party Site. Coinbase is providing these links to you only as a convenience, and the inclusion of any link does not imply endorsement, approval or recommendation by Coinbase of the site or any association with its operators.

Unless otherwise noted, all images provided herein are by Coinbase.

Things You Need to Know about the Bitcoin Halving, Ethereum’s Competitors Nearing Launch, and… was originally published in The Coinbase Blog on Medium, where people are continuing the conversation by highlighting and responding to this story.

from Money 101 https://blog.coinbase.com/things-you-need-to-know-about-the-bitcoin-halving-ethereums-competitors-nearing-launch-and-f8b25acc127f?source=rss----c114225aeaf7---4 via http://www.rssmix.com/

0 notes

ashleymth229-blog · 8 years ago

Text

Types of problems used in the classroom

For my third blog post I am going to discuss the importance of group activities, application problems, and practice problems in the classroom. I am going to first discuss application problems in the classroom. Recently in my Math 229 class we were able to choose from a list of activities in order to explore our knowledge and understanding about logs. My group chose to work on Sprikinski maps, which are designs that can be made to fit logarithmic functions on a graph. It was a very cool activity because you spent part of the time coloring your design and the other time was spent finding an equation to fit our data. I didn’t realize that it would be as simple as plotting points based off of how many empty squares I had and finding an equation to fit. I think this would be an excellent activity to do in my classroom with my future students because they would have no idea that they are doing logs until I had them fit an equation to the data from their picture. Another group in class was working on finding a log function to fit data that had to do with blood glucose level and medications. This type of activity would answer the over arching question high school students face of “when will I ever use this again?” This would show them that logs are applicable in different fields of study and that it could affect everyday life. The last application problem we discussed was the gros rate of movies at the theaters. It was really cool to see how each weekend the movies would decrease in the amount of money they would bring in. I was shocked at the exponential decay rate of the money they brought in, and it was interesting to see how normal movies fit this pattern but how some films don’t fit this pattern. I believe this would be an amazing tool to use in my classroom to keep students interested in the topic.

My Second topic of discussion is group activities in the classroom. I think they are a very important tool, when trying to help students understand what they are learning. One activity that I thought was very beneficial to do in a group was explaining why the log rules work, and how they are connected. My group discussed why log(x^2) and 2logx are the same. We discussed how x^2 is the same as x times x which means that it could be written as log(xx). You would need to grasp the rules of logs such that you would know you could split log(xx) into log(x)+log(x) which would be the same as 2log(x). At first when someone at my table brought up this concept I had no idea how they came to this conclusion. They wrote out their explanation and I was better able to understand their thinking which helped me learn how this concept worked. I think that being able to discuss this problem with my group was helpful because I was able to ask questions without having the fear of seeming stupid in front of the class. I think a lot of students get confused in activities but are too afraid to say anything in fear that they will be the only one. So I believe that using group activities help students to have a safe space to ask questions because its less embarrassing to ask a peer than it is to ask the teacher in front of the class.

The last type of activity that I would like to discuss in the classroom is the idea of practice problems and worksheets. I think that these are beneficial when the student already has a good basis of understanding, but overall are just drill methods. These help students practice so that they know the material but rarely challenge them to go further than just computations. I think that students get tried of these activities more than others but are necessary in order to test their basic understanding.

To conclude, I believe that group activities, application problems, and practice problems are all beneficial in the classroom. I would like to do a lot of group work and application problems in my future classroom because I think that they help create a deeper understanding of the content. I think they also promote a safe space to ask questions if they are confused. I also think that practice problems are necessary to assess understanding and to help further growth and practice, however I would like to limit them in my classroom and have them used as more of a homework activity rather than an everyday in class activity.

2 notes · View notes

realtalkgames · 5 years ago

Video

The Forrest (GAME EXPLAINED)

This is a guide to the story in The Forest. The story is currently more or less complete, though the game developers will probably still add to it. This page attempts to place all the assorted story pieces in chronological order. It mostly covers major events, as the rest of the story is left somewhat unclear. The story is the background of the game. Much of the story is optional, and in many cases, can be completely ignored while still beating the game, such as in the case of a speed run. Many story items can be found that add to the story, some of which can be added to the survival guide in the notes section. In the to do list, the first task listed is 'Find Timmy'. This prompts the player to begin exploring the peninsula and to advance the story. Ending the game unlocks creative mode. After ending the game, the player can continue playing to the same save file. The Peninsula It is assumed that The Peninsula is located in Canada or another similar northern location, due to the climate, animals, geography, and location of the developers. It comprises the majority of the setting for The Forest and includes both an extensive below-ground cave system and large mountains, in addition to the basic forest floor. It is assumed that the caves suffer regular cave-ins, due to both the sounds the player can hear while in the caves (rocks tumbling) and the fact that several bodies (such as the Christian Missionaries below) are in an area only accessible by the rebreather yet come from a time period without such technology. The Ancient Ones Across the island, ancient-looking obsidian doors, artifacts - such as the Obelisk - and structures can be found. Some of these structures require sacrifices of some sort, including live human beings. These suggest a 'Lovecraftian' sort of ancient power. As well as that, mummified corpses can often be found near and around the doors, corpses that were left alone by the cannibals, suggesting the doors and the things found near them predate the cannibals (or perhaps the corpses weren't good to eat). This suggests that the use of the resurrection obelisk produces misshapen mutants, such as the Armsies, Virginias and mutant babies, (also seen prior to the boss fight with Megan Cross), and that it has been used before the first truly notable visitors - the missionaries - came to the peninsula. For reference, please see the Virginia Sketch and the Latin Paper. Christian Missionaries At some point (probably late 19th or early 20th century), many Christian missionaries or priests came to the peninsula. The Latin Paper, presumably belonged to said Christian missionaries, can be found in an abandoned camp in Cave 1 surrounded by aged items such as raw dynamite sticks. The Virginia Sketch almost certainly belongs to the missionaries, as it is drawn in the same fashion. It can be found near the grey tents with Bibles and crosses that seem to be a hallmark of the missionaries, along with being near lots of mummified corpses, praying to an obelisk drawing. Due to the presence of the Latin Paper, it can be assumed that the group of missionaries were Roman Catholics or similar, including someone with decent knowledge of church Latin. They left many Crucifixes scattered around the place, along with crosses projected on to walls sometimes near their heavily decayed and mummified corpses. Bibles too are a frequent find near their old camps and inside the caves next to the corpses. Their corpses are often left alone and mummified, which suggests a sudden catastrophic event which led to their death. According to the Latin Paper, the Missionaries encountered a four-legged woman, most likely referring to Virginia. This would mean that mutants at least were already on the peninsula at this point, further pointing towards the artifacts as the cause of the mutants. Sahara Sahara Therapeutics purchased the peninsula at some point to conduct its experiments on "eternal life" and resurrection through the obelisks, and built a complex system of offices and research labs, stretching as high as the mountains to deep below the ground into the caves. The Jarius Project was probably first marketed as a program, whose aim was to heal terminally ill children. These initial test subjects may have been sick children whose parents had volunteered them for participation in clinical trials at the facility where they were relocated to and continued receiving medical treatment. It's possible that Dr. Matthew Cross began experimenting with the artifact by using a living child to revive one that had died. However, this would in turn result in the death of the submitted child, who themselves would subsequently need to be revived at the cost of another, thus creating a cycle of child sacrifice and resurrection. After the process, they were placed in observation rooms where they began to develop genetic mutations ranging from grotesque physical deformities to highly exponential growth rates. These genetic mutations were isolated and studied for their possible applications in other fields, such as cloning and adult longevity. At some point, something went terribly wrong in the lab, as shown on one of the camcorder tapes; an Armsy escaped from its containment, which possibly led to a cannibal/mutant uprising that left the facility overrun. Almost all human inhabitants are gone, leaving behind decaying corpses, bloody body parts, and a few live mutants and cannibals. This suggests that this has happened fairly recently, as the head scientist Dr. Cross can be found at the end of the game, dead. Presumably killed by his daughter who stuck crayons into him. Missing Children A newspaper clipping can be found with the headline "Siblings Still Missing" in Cave 3. A milk carton can be found on the Yacht depicting Zachary, another missing child. It can be assumed that either Sahara took the children while the lab was still functional, in order to experiment on them, or to use the resurrection obelisk. Assorted Visitors There are many Abandoned Camps scattered across the The Forest. These groups include, but are not limited to: Cave Divers. Diving camps can be found deep in the caves, in sections only accessible by using the rebreather. Cave climbers/explorers. They have tents inside the caves as well in the non-water portions, along with some tents on the inside wall of the cenote. Hikers/explorers. Their sleeping bags and tents can be found all over the forest topside. Film Crew. They have a larger established camp with modern tents and film equipment scattered about, with scripts for a "Survivor" type program to be found on the ground nearby. These groups seem to have visited the forest at assorted times and to all have been cannibalized with no survivors. Yacht Family At some point, a yacht crashed in a small bay on the west side of the peninsula. This yacht seems to have arrived in 1984 or later. Supporting evidence includes the yacht magazine dated to 1984. On rare occasions Matthew Cross can be seen walking around on the yacht, so he may have a connection to it, or perhaps he uses it as a temporary shelter. Several drawings made by his daughter Megan Cross can also be found. Matthew Cross and Family The exact sequence of these events is unclear and could paint radically different pictures of Matthew Cross depending on their order. For some period prior to the lab's downfall, Matthew worked for Sahara Therapeutics as head of the Jarius Project, researching the resurrection obelisk as indicated by his credit in Orientation Slideshow #2. He was at least aware of the power obelisk, as referenced by an email that he sent noting that it could take down a plane. This suggests that with his knowledge of the power obelisk's ability to take down planes and the resurrection obelisk's ability to revive dead children, he took down the plane the player starts the game in, in hopes of acquiring a live child, and uses said child in the ultimate goal of reviving his daughter. He had a wife called Jessica, who divorced him at some point, along with filing a restraining order against him. According to the dates on both the restraining order and the Autopsy Report, the restraining order was filed 3 months before Megan's death, although the year is unknown. The restraining order also specifies "the father will have no contact with mother or daughter." It is unknown whether Jessica was aware of the full nature of his work at Sahara Therapeutics. Megan appears in a Camcorder video showing her alive and in a wheelchair in what appears to be the Sahara Lab's Cafeteria with many other people present. Another video shows Megan, again in a wheelchair, present during the escape of an Armsy. The autopsy report can be found and picked up which shows that Jessica was murdered in a homicide by multiple stab wounds and head trauma. Matthew eventually gets fired from the lab for unethical and inappropriate use of company equipment, presumably tinkering with the resurrection obelisk. Matthew is on the peninsula alone (except for the cannibals), and he decides to use the power obelisk to bring down an airplane to steal a living child (Timmy) to revive his daughter. He is the red man which is seen by the player after the plane crash. The red paint acts like a protection from the cannibals. The Player The protagonist who you play as is Eric LeBlanc. He appears to have adept survival skills, as he can build shelters and go hunting within a short amount of time after the plane crash, with nothing but a handheld axe and an outdoor survival book. He appears to be a reality TV star, as found from a magazine cover. This magazine also suggests his wife is dead. He is most likely a TV survivalist, similar to Bear Grylls. He has one son, Timmy. The Plane Crash The plane may have originated from New York, as certain passengers are wearing "I ♥ NY" shirts and suitcases contain statue of liberty figurines. It is assumed that the plane is predestined to arrive in Germany, because the label on the plane resembles the logo for the German airline "Lufthansa". The plane was carrying many tennis players, who had balls and rackets in their suitcases. The plane crashes after experiencing sudden storm-like turbulence and engine failure. Some indeterminate time after the crash, a man in red paint (Dr. Matthew Cross) takes Timmy away while the player futilely crawls towards him. Only Timmy, the dead stewardess, the red man (Dr. Cross), and the player(s) are present on the plane when the player wakes after the crash, suggesting any dead had already been taken by the cannibals. The mostly intact condition of the rear section of the plane make it possible that many other passengers could have survived, but that they had already fled the area, possibly upon the death of the stewardess. Their scattered locations across the peninsula suggest that some may have survived as long as several days before falling prey to the cannibals. Finding Timmy The player explores the peninsula to great extent, gearing up to head to the bottom of the sinkhole. The Vault, found at the bottom of the sinkhole, can be opened with the keycard. It leads to the research lab. After exploring much of the lab, the player finds the Resurrection Obelisk, with the dead Timmy inside. The obelisk/machine prompts him for a sacrifice when Timmy is hooked to an operating table. The player then realizes that Matthew had kidnapped Timmy to use as a sacrifice to bring Megan back to life. The player goes on a hunt for Megan, finding many of her childish drawings that are just like Timmy's. He encounters a dead Matthew Cross, with crayons shoved inside his eyes and mouth. A Megan Drawing suggests that Megan saw her father as a scary red monster, possibly giving motive for Megan killing her father. Megan is finally found, surrounded by drawings and toys. She flies a toy plane through the air before crashing it to the floor and pointing at the player, suggesting she knows who he is. Megan then suffers a seizure and transforms into a boss mutant that behaves and looks similar to a Virginia, including the spider legs and mutant babies. After defeating Megan, the player takes her corpse back to the artifact, only to find out that a live sacrifice is required. The player then uses a new keycard found on Megan's body to go to a second artifact. This one has the power to crash planes, seemingly by using an EMP. The player can then choose to use this power to bring down a plane or shut down the device and let the plane pass safely. Happily, Ever After? After taking down the plane, the screen cuts to black with the text "One Year Later". The player and his son are being hosted on a talk show, where the player competes in a friendly tree chopping contest with the host, known as Doran. It is assumed that the player did the same thing that Matthew did, kidnapping a child, and resurrecting his son. During the cut scene, Timmy is shown to be having small tremors and shakes. The happy music turns to horror as Timmy begins to have a violent seizure on the ground, implying that he will undergo a mutation just as Megan did. The character rushes over to comfort Timmy. Timmy's spasms suddenly stop, and he looks up at his father, the player, and smiles. It immediately cuts to black and the credits begin to roll, The next scene appear within Timmy's perspective as he is now a young adult, in his small apartment, he looks over his bulletin board with a map of an unknown island (with a possibility that said island has a link to future plot). Scene ends in another cliffhanger as Timmy goes into seizure again. He walks to his window, overlooking a city. Alternate Ending If the player chooses to shut down the device, he will leave Timmy behind (even more signified as he burns his remaining photo of Timmy) and return back to the island with the possibility of being rescued (albeit without Timmy with him). The game will return to normal with pacification and horde mode unlocked via secret artifact, and a 5 new craftable decoration.

1 note · View note

shirlleycoyle · 5 years ago

Text

A Complex Systems Theorist Explains How We Can Stop Coronavirus

The coronavirus pandemic is terrifying, but the solution is almost shockingly simple: We have to stop spreading the virus. In fact, if every single one of us took extreme social distancing measures and all of the sick were isolated, the curve we’ve been attempting to flatten would start plummeting toward zero.

While a gradual increase of COVID-19 cases that don't overwhelm healthcare followed by a decline is the goal of most public health agencies, basic math suggests we can actually turn exponential growth into exponential decline quite rapidly.

That’s the perspective that Yaneer Bar-Yam, a complex systems scientist who uses his specialized branch of mathematics study systems with many interactive components, like the stock market or social movements, is attempting to share with the world. His field’s basic premise is that all of the interdependencies within complex systems result in various "tipping points" and non-linear responses that are difficult to describe using simpler mathematical models. Over the last few months, Bar-Yam’s research organization, the New England Complex Systems Institute, has produced a series of coronavirus-focused white papers and guides that use the fundamental dynamics of a global pandemic to explain how to stop it.

In a short explanatory paper published online last month, Bar-Yam shows how pandemic spread is a simple problem of matrix multiplication. If you haven’t brushed up on your high school algebra in a while, a matrix is just a set of numbers arranged in rows and columns. In this case, the matrix is a “contagion network,” with columns and rows representing different individuals in a population. If two individuals interact enough to spread the disease, the value where their row and column meet is one. Otherwise, it’s zero.

In an ideal scenario where we know exactly who’s sick and who’s not, this contagion network could be multiplied by the list of people who are sick—a column of ones (sick) and zeros (healthy)—to produce a new list showing who’s likely to be sick during the next infectious period. Repeat the process over and over, and the illness either spreads or declines over time.

Critically, which of those two paths a virus follows, growth or decay, depends on the connectedness of the contagion network. Epidemiologists use a variable called R0, or the number of people each sick person infects, to describe this connectivity. If R0 is greater than 1, the number of sick will rise over time; if it’s less than one, the sick cases will shrink.

For now, estimates for COVID-19’s R value (called the “effective R” when it’s measured in populations) vary from around 2 to nearly 5. Either end of this range indicates a disease capable of spreading exponentially, which is exactly what we’re seeing in the US. But Bar-Yam’s math also demonstrates that if everyone on Earth were to self isolate for a couple of weeks — either alone, or with family members who also aren’t sick — COVID-19 would run out of new hosts to infect, and the pandemic would be brought under control. In a best-case scenario, effective R would fall to zero, and the illness could be eliminated in a single infectious period—in this case, about two weeks. In essence, instead of flattening the infection curve we’d be arresting it.

“The point is, it’s a multiplicative process and that creates an exponential growth or an exponential decline,” Bar-Yam told Motherboard. “The trick is if you have an exponentially growing disease, [switch it] to make it exponentially declining.”

Everyone eliminating all contact outside the home is impossible, of course, meaning we can’t realistically expect to vanquish the pandemic in just a couple of weeks. Health care workers risk infection simply by treating the sick; workers at elderly care facilities can’t easily abandon all physical interaction with their charges. We still need people working closely together in emergency services, running power plants and sanitation systems, and much more. Society can’t just cease to function.

But altering the contagion network in order to drive the effective R value down and change COVID-19’s trajectory from one of exponential growth to exponential decay is far from impossible. In fact, several countries have been able to do just that, most notably China, which was able to exponentially bend its infection curve toward zero through widespread testing and contact tracing, isolating the sick, and placing over fifty million citizens on lockdown. While China was seeing thousands of new cases of COVID-19 a day at the height of its outbreak in late January, on Monday it only saw one new local infection, at least according to official numbers from the National Health Commission.

“China’s taken criticism for coming in late,” said Shannon Bennett, a microbiologist at the California Academy of Sciences. “But when they did decide to do the social distancing they came in hard. Now they’re still getting new cases per day but fewer and fewer.”

However, if math tells us that countries with exponentially-rising caseloads can flatten and reverse their infection curves through collective action, other aspects of complex systems behavior lead to more sobering conclusions. For one, there’s the issue of time delay: It might take days to weeks for our responses to COVID-19 to start having a demonstrable impact. All the while, the number of cases is likely to keep rising fast.

Bar-Yam noted that even though China began taking aggressive control measures when there were fewer than 1,000 officially-reported cases in the country, by the time the outbreak was under control, the number of cases had topped 80,000.

As of Wednesday morning, The New York Times’ database indicated nearly 6,000 coronavirus cases in the United States, but Bennet and other experts have said that number is likely a severe underestimate due to inadequate testing. Unfortunately, this suggests that if the U.S. took immediate and radical nationwide action—as we saw the Bay Area do yesterday, when officials ordered nearly 7 million people to go into a near-lockdown—the scale of our outbreak would still likely be considerably worse than China’s.

“I would definitely say we are on the exponential part of the curve,” Bennett told Motherboard. “The power function of that exponential increase I would say is still uncertain, and certainly hampered in its estimation by the fact that we have a mess going on with under-testing.”

Complex systems also have tipping points that cause them to go through “phase changes,” as Danny Buerkli, the co-founder of Swiss government innovation lab Staatslabor, noted in a recent blog post on how this branch of math is relevant to coronavirus. In this case, a tipping point might be when hospitals run out of beds or critical equipment, forcing the entire healthcare system to go into triage mode.

“We’ve seen the [health care system] overload happening in China, Italy, possibly elsewhere,” Buerkli told Motherboard. “It’s misleading to think that just because everything is OK now it will be in the future."

In the U.S., we (hopefully) still have time to prevent COVID-19 from crossing a dangerous tipping point where the healthcare system is overwhelmed. But the clock is ticking. Bennett noted the importance of rolling out more widespread testing immediately; Bar-Yam, meanwhile, emphasizes the role of personal behavior and individual responsibility through aggressive social distancing, practicing good hygiene, and self-isolating at the first sign of symptoms. Businesses also have a key role to play by telling their employees work from home or providing paid time off (a challenge many companies aren’t exactly living up to).

All of these measures, Bar-Yam says, will help to weaken the contagion network and steer us onto a new, far less terrifying trajectory.

“In our current context, the network is connected everywhere and gets transited very rapidly,” he said. “But it’s possible by changing how people behave to radically prune that network."

A Complex Systems Theorist Explains How We Can Stop Coronavirus syndicated from https://triviaqaweb.wordpress.com/feed/

0 notes

muabannhadatdananggiare · 6 years ago

Text

New Article Reveals the Low Down on Exponential Growth Biology and Why You Must Take Action Today

The Downside Risk of Exponential Growth Biology

This course supplies you with many practical examples so you can definitely see how deep learning may be used on anything. The bacteria-in-a-flask instance isn’t truly representative of the true world where resources are usually limited. Running replicate samples is almost always a very good idea.

You’ve been tasked with determining whether you should create a new city hall. Obviously, most banks aren’t nice enough to supply you with the greatest possible pace. Both strategies minimize the odds of getting eaten.

Let’s start by viewing a fundamental system which doubles after a quantity of time. If all works properly, we’re only term paper writing service speaking about a couple of minutes from the top level manager’s day to manage the reporting of the underlying systems. Although Davis saves most of his analysis and discussion for the third region of the book, he doesn’t be afraid to adjudicate briefly on specific issues as they arise in the prior parts.

The Do’s and Don’ts of Exponential Growth Biology

The access to limited resources can’t demonstrate an exponential growth. There’s no other aspect to disturb the intrinsic development of the people. The exponential growth happens when plentiful of resources are obtainable for the individuals in the people.

Competition is often regarded as absolutely the most important biotic factor controlling population density. Growth prices are trickier and not everybody employs the term the way that they are supposed to (even I sometimes become sloppy with the terms!) Consistent growth builds up as time passes.

In these two scenarios, the equilibrium population of 1000 is reportedly stable. Over long spans of time, genetic variation is more easily sustained in massive populations than in modest populations. As an example, density could be measured as the range of trees per hectare or the range of wolves per square mile.

At any particular time, the real-world population comprises an entire number of bacteria, even though the model takes on noninteger values. A sample is merely a subset of the populace. Especially take a look at the population data sheet.

https://biblioteca.ulpgc.es/

The problem isn’t specifically the rarity of events, but instead the prospect of a little number of cases on the rarer of both outcomes. When considering growth above a period of years, it is necessary to be aware that taking the natural logarithm of the proportion of the last value to the initial price and dividing by the period of time in years gives the typical yearly growth rate. To begin, here are a few data for the earth’s population in late years which we’re going to use in our investigations.

As your company grows you have to develop scalable management and superior control systems. You’re able to run the chance of certain data being leaked, resulting in severe consequences like brand discredit, and even legal consequences for the business. Of course, if it is not doing well, your calculations may very well be correct.

The Pseudo-R2 in logistic regression is best utilised to compare unique specifications of the exact model. Although the exponential function may start out really, really small, it will gradually overtake the development of the polynomial, as it doubles all of the moment. The logistic model is appealingly easy and adequate for some scenarios, but it’s far too generic to capture different phenomena.

A decision to maintain a variable in the model might be contingent upon the clinical or statistical significance. In any event, be fluent in both models and learn how to hop between both. grademiners.com/dissertation-methodology If our model is allowing impossibly significant growth values, it could be an indication that we’ve forgotten an important constraint on the computer system.

From the view of assessment, failures aren’t welcome. A paper isn’t unusual in businesses when they need to get all the feasible perspectives and’re attempting to have a remedy and data out there. More information about solving this scenario are offered in this video.

Exponential Growth Biology Help!

The rate of change of the quantity of water in the tank is dependent on the quantity of water in the tank. The number of individuals a particular habitat or environment can support is referred to as the carrying capacity. In summary, unconstrained all-natural growth is exponential growth.

Whether there are sufficient glucose utilization enzymes in the first cells, it is advisable to skip lag1 and commence growth immediately. Traditionally, 17 x 100 millimeter round-bottom tubes are used for best outcomes. In the event the cells are in a hypertonic environment, they will wind up plasmolyzed and won’t contain enough water to do cellular functions.

In the latter circumstance, the rates of cell division and of the growth in cell size differ in various pieces. Many nations have attempted to lessen the human influence on climate change by decreasing their emission of the greenhouse gas carbon dioxide. The gain in the cell dimensions and cell mass during the evolution of an organism is termed as growth.

This formula is utilized to illustrate continuous rise and decay. You’re probably going to wish to also determine the number of the material you’ve detected. The above mentioned experiments were repeated independently 3 times.

Otherwise, it can normally be soldat a profitprovided the owner recognizes their limitations soon enough. Our experts utilize exceptional content to finish the assignments. Not all your sales team are employing the exact same scripts.

Today we’re very happy to declare that we’ve found an extremely intriguing content to be discussed. Our Remote Freight Bill Entry Solution extends to you the next benefits. They can ask for our service in any type of academic-related issues.

Bài viết New Article Reveals the Low Down on Exponential Growth Biology and Why You Must Take Action Today đã xuất hiện đầu tiên vào ngày Nhà Đất Đà Nẵng.

source https://muabannhadat.danang.vn/new-article-reveals-the-low-down-on-exponential-growth-biology-and-why-you-must-take-action-today-3605.html

0 notes

enetarch-math · 8 years ago

Text

Chapter 6.1 Exponential Functions

Let’s pick up on a topic we started in Chapter 1.4 - Exponents.

Up till now exponents have been represented by the letter (n) in equations, like: (x^n). (n) represents the number of times (x) is times by itself (x *x *x *x ...) = (x^n). When we discuss Exponential Functions, we are describing functions where (x) is the exponent of the function, and changes. (c^x). Where (c) is a constant, and (x) is the variable.

F(x) = c^x, or y = c^x.

There are a few laws that help us work with exponents:

c ^ 0 = 1

c ^ 1 = c

(c ^ x) * (c ^ y) = c ^ (x + y)

(c ^ x) ^ y = c ^ (x * y)

(c ^ -x) = 1 / c ^ x

(c ^ x) / (c ^ y) = c ^ (x - y)

(c * d ) ^ x = (c ^ x) * (d ^ x)

( c and d ) in these expressions are known as the base. ( x and y ) are the exponents.

Now let’s look at some places where (c ^ x) is used in daily life.

Evaluating an Exponential Function

Let’s start by setting (c) in (c ^ x) to a number other than one (1). Since (1 ^ x) is still (1). So, let’s try two (2).

c = 2

y = c ^ x, produces the following graph ...

Now consider different values for (c), other than 0 and 1. Over time mathematicians found that a particular value of (c), also known as a base, seems to stand out above all others.

Let’s change (c) to (c + h), where (c) is still a constant value, and (h) can change, into smaller and smaller units. So (h) could start at one (1) and decrease to .0000000001. Another way to express (h) is as (1 / n), where (n) is a number between one (1) and infinity.

for n = 1 to infinity

h = 1 / n y = (c + h) ^h

What mathematicians find interesting is that (y) eventually equals 2.718.... They have named this value (e). (e) is short for exponent.

Application of Exponents

In this example, we will use a standard banking interest calculation to show you that (e) is hiding in it.

accrued = principal * (1 + rate / period) ^ (period * time)

Principle .. is the amount of money you are starting with.

Rate .. is the interest rate that banks are providing when you loan them your money.

Period .. is the number of times your money will be compounded, increased with earned interest. It the interest compounded every 6 months, every month, every week, or every day?

Time .. is the number of years that you have loaned your money to the bank.

Accrued .. is the expected amount you expect returned when your deposit matures.

Now let’s transform [ accrued = principal * (1 + rate / period) ^ (period * time) ] into [ y = a * (c + 1 / n) ^ (n * t) ]

Accrued is (y)

Principal is (a)

(1) .. is (c)

1 / (Rate / Period) is (1 / n)

n = Period / Rate

Period = Rate * n

Now let’s substitute the various letters into the equation for calculating banking interest. Where possible I will shorten names to letters, example time is (t).

accrued = principal * (1 + rate / period) ^ (period * time) y2 = a * (c + 1 / (period / rate) ) ^ (period * t ) y2 = a * (c + 1 / n ) ^ ( (n * rate) * t ) y2 = a * (c + 1 / n ) ^ ( (n * r ) * t )

Now with a bit of mathematical transformations using the laws provided above, let’s find (e).

I used (y2) in the previous equation, because I want to distinguish the equation (y) evaluates to, when we see it.

y2 = a * (c + 1 / n ) ^ ( (n * r ) * t ) y2 = a * (c + 1 / n ) ^ ( n * r * t ) .. removed parentheses y2 = a * [ (c + 1 / n ) ^ n ] ^ ( r * t ) .. added brackets to group an expression

Let’s look at this grouping a little closer using the rules of exponents. There are three (3) transformations happening here:

(a * c ^ n) is the same as (a) * (c ^ n)

[c ^ ( n * r * t ) ] is the same as [c ^ n] ^ ( r * t ) )

brackets, as exemplified above, help us see the expression we are looking for .. [ (c + 1 / n ) ^ n ]

Now let’s substitute (y) for our equation.

y2 = a * [ y ] ^ (r * t)

y = (c + 1 / n ) ^ n .... this is the equation for (e), from above.

Now that the expression of (y), [ (c + 1 / n ) ^ n ], looks identical to (e), let’s substitute (e) into the equation and see what it looks like.

y = (c + 1 / n ) ^ n

y2 = a * [ y ] ^ (r * t)

y2 = a * [ e ] ^ (r * t)

Now you can consider various interest rates, periods of compounding and time frames to see which will give you best return on your investment. But as always, make sure that your initial principle is protected.

Application of Exponents, #2

Exponential grow of bacteria colonies is calculated using (e). Where [ y = c * e ^ (k * t) ].

(t) is amount of time a colony was allowed to grow.

(y) is the number of cells or population size after some time (t).

(k) is the growth rate. How many cells will subdivide in a period of time (t).

y = c * e ^ (k * t)

Application of Exponents, #3

The half life of radio active materials is calculated using (e). Where [ y = c * e ^ (-k * t) ].

(t) is amount of time the material was allowed to decay.

(y) is the number of atoms left to decay after some time (t).

(-k) is the decay rate. How many atoms will decay in a period of time (t).

y = c * e ^ (-k * t)

#precalc #exponents #growth rate #decay rate